How I Built Software Renderer from Scratch

Computers are fantastic at processing, producing, and consuming data. But I've often found that the most difficult part of the pipeline is representing the data to a user. This can often take the form of bar charts or scatter plots, but there are situations where they just don't fit the bill.

3D graphics enable developers to create interactive programs that appear most similar to the natural world. By presenting a three-dimensional space, the barriers for entry drop. I wanted to learn more about how this worked.

Inspiration

For a long time, I've been told that the most prevalent application of linear algebra was computer graphics. Before I even began my independent study, I knew I would eventually get around to doing something like this.

One of the big roadblocks was the amount of technical know-how I thought it required. You see, most 3D programs do all the number-crunching on the specially designed graphics processing unit that is readily available on most modern computers. From my previous attempts to use GPUs, I knew setting up the pipeline is quite involved, with much math.

Since I wanted to focus on the math, I postponed the project. That is, until it occurred to me that I could simply not use the GPU. I know it might sound obvious, but it felt so freeing at the time.

What Are Software Renderers?

A software renderer is, as it may sound, a renderer that does all computation in software. No specialized hardware is utilized at all.

Demo

Before I get into how it works, I want to give you the chance to try it out yourself. I've created a very simple scene to demonstrate.

Function	Key
Look Around	Left Mouse Click
Toggle Depth Buffer	R
Toggle Face Sorting	O
Toggle Backface Culling	B
Increase FOV	Arrow Key Up 🔼
Decrease FOV	Arrow Key Down 🔽
Move View	W, A, S, D

Explanation

Note

In this article, I intend only to talk about the math related to the problem. If you are interesting in the nitty-gritty how lines and shapes get drawn to the screen, I suggest you read up on Bresenham's line algorithm, Xiaolin Wu's line algorithm, and Drawing Filled Triangles

Projection

With a perspective camera, projection happens from the world, towards the "sensor," which is a fixed point. For the sake of argument, let's say that point is at the origin and the camera is facing the positive $z$ axis.

We want all other points to be projected onto a plane $d$ distance away. If you are a photographer, $d$ will be the focal length of the camera.

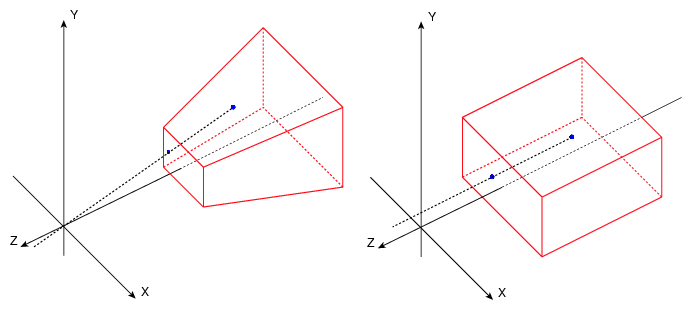
Orthographic Projection

In the case of orthographic projection, this is easy. Because we have placed the camera on the origin, facing the positive $z$ axis, we can draw the coordinates of any given point directly to the screen. The only consideration necessary pertains to the points behind the camera, which we can skip by checking the sign of the $z$ component.

Homogenous Coordinates

This is where homogenous coordinates come in. When working in euclidean space, we represent a given vector or coordinate using three components:

When we are working in projective space, we can represent any given vector or coordinate using four components.

We can convert between these formats interchangeably. To convert a homogenous coordinate to euclidean, divide all other components by $w$:

We can transform any euclidean coordinate to a homogenous coordinate by setting $w = 1$

Just like we can perform various transformations on euclidean coordinates, we can perform similar ones on homogenous coordinates. The major difference: instead of requiring conventional additions or subtractions, homogenous coordinates can be translated via matrix multiplication.

For example, let's say we have a point at the origin, and we want to perform both a translation and rotation. If we were using euclidean coordinates, we would have to translate it via addition, then rotate it separately.

In homogenous coordinates, we can do it with a single matrix operation by preparing the matrix ahead of time:

By condensing the entire transformation into a single matrix, we are able to save a ton of computing time.

Perspective Projection

The essential idea of perspective projection is simple: we want points further from the camera to appear closer to the $z$ axis the further away they are. Remember that $d$ is the surface we are projecting onto. This is possible with homogenous coordinates with the following matrix:

Assuming you have an understanding of matrix multiplication, it should be apparent why this works. When the $w$ component of the matrix is being computed, the $z$ component will be divided by $d$. The result then becomes a divisor of $w$, which affects all components of the resulting vector due to the nature of homogenous coordinates. In short: $w \leftarrow w * (-z / d)$

Color

Now that we've established exactly how to project points in space onto the screen, we need to start coloring in triangles. As I said before, I am not going to go into the algorithms that do this. I want to discuss how to determine the color to fill in.

We could just choose one solid color. As you can see from the demo (by pressing R), this doesn't lead to a particularly impressive or visually pleasing result. I want an additional way to convey depth.

Given the three points that make up a triangle $p_1$, $p_2$, and $p_3$, we can find its normal vector (the vector perpendicular to it's surface), $\vec{n}$ fairly easily.

Note: the vertical bars around a vector $||\vec{v}||$ signify getting the vector's length.

Now that we have the triangles normal, we can fill it in more brightly depending on how directly it is facing the camera.

The resulting shading is the default in the demo.

Alternatively, we can also simply color based on the distance from the camera. The resulting image is called a depth map.

Sorting

When the program is supplied a mesh, the faces are not in any specific order. If we were to just draw each face in the order it arrives, nothing would make sense.

To solve this, we simple sort each face by it's distance, then draw the furthest faces first.

If you want to see what it would look like, go to the demo and press O to toggle face sorting.

Optimization

There are countless ways to optimize a renderer like this. They all involve work-avoidance. The one I want to discuss is often referred to as backface culling.

In most situations, there is no need to see the inside of a mesh. This allows us to avoid a lot of work for very little effort. By checking the alignment of the point-to-face vector with a face's normal, we can check if a given face is facing toward us or not.

In the demo, you can toggle backface culling with B.

Conclusion

When I initially designed this project, I hoped it would allow me to apply some of the more advanced Linear Algebra concepts that I've learnt in the second trimester. In this regard, it did not live up to my expectations.

While I was allowed to explore some concepts, like orthogonality, it was not quite satisfactory.

It was not for naught, though. I learnt a lot about the fields of math and computers integrate together, as well as how to more effectively convert mathematical concepts into a working prototype. I want to continue doing projects like this, and cannot wait to re-take Linear Algebra when I go to college.